Mathematics for AI: Functions

A function is a rule that maps each element from one set—called the domain—to exactly one element in another set, known as the codomain. A set holds a collection of things. For example, here’s a set A that holds three colours:

A = { red, green, blue }

Function Notation

To define a function f from a set A (domain) to a set B (codomain), we write:

$f:A\to B$

Here:

• f is the name of the function
• A is the domain (i.e. the set of inputs the function accepts)
• B is the codomain (i.e. the set of possible outputs)

In simple terms, this notation tells us that the function f takes elements from set A and maps them to elements in set B.

A Worked Example

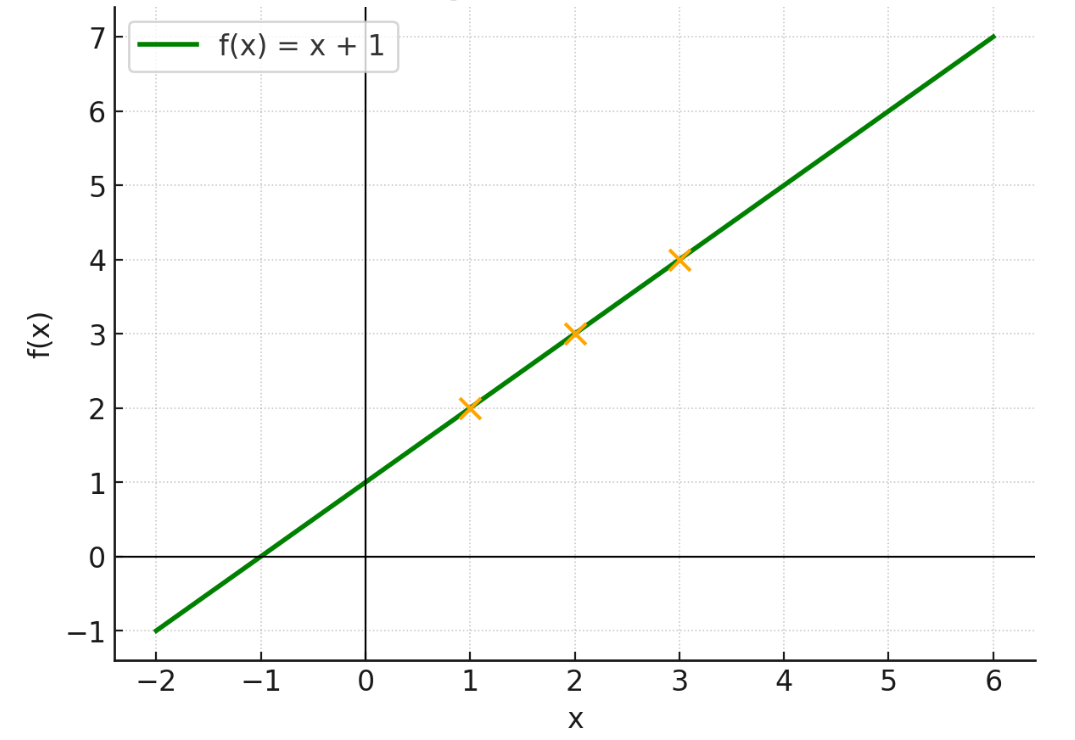
Let’s say we define a rule:

Take any number and add 1 to it.

That’s our function. Now, apply this rule to some numbers:

• If you start with 1, you get 2
• If you start with 2, you get 3
• If you start with 3, you get 4

Every input gives exactly one output.

We write the function mathematically as:

$f\left(x\right)=x+1$

This means:

• f(x) is the output of the function when the input is x
• The rule is: add 1 to whatever x is

Now, let’s say our input values (i.e. our domain) are:

{ 1, 2, 3 }

Apply the function to each element:

x	f(x) = x + 1
1	f(1) = 1 + 1 = 2
2	f(2) = 2 + 1 = 3
3	f(3) = 3 + 1 = 4

Graph of f(x) = x + 1: