Mathematics for AI: Unit Vectors

A vector has both a magnitude (or length) and a direction. A unit vector is a vector with a magnitude of 1 pointing to some direction.

Unit Vector Notation

Unit vector notation uses a hat symbol ^ to show that the vector has a magnitude of 1. For example:

$\hat{v}$

"v-hat" is a unit vector that has a length of 1 and points in some direction.

Unit vectors lie along the axes of a Cartesian coordinate system.

Unit Vectors in 2D Space

In 2D space, we use two unit vectors to show direction along the x-axis and y-axis.

$\hat{i}\text{ - unit vector in the x-direction}$ $\hat{j}\text{ - unit vector in the y-direction}$

These vectors each have a magnitude of 1:

$$\hat{i}=[1,0]\hat{j}=[0,1]$$

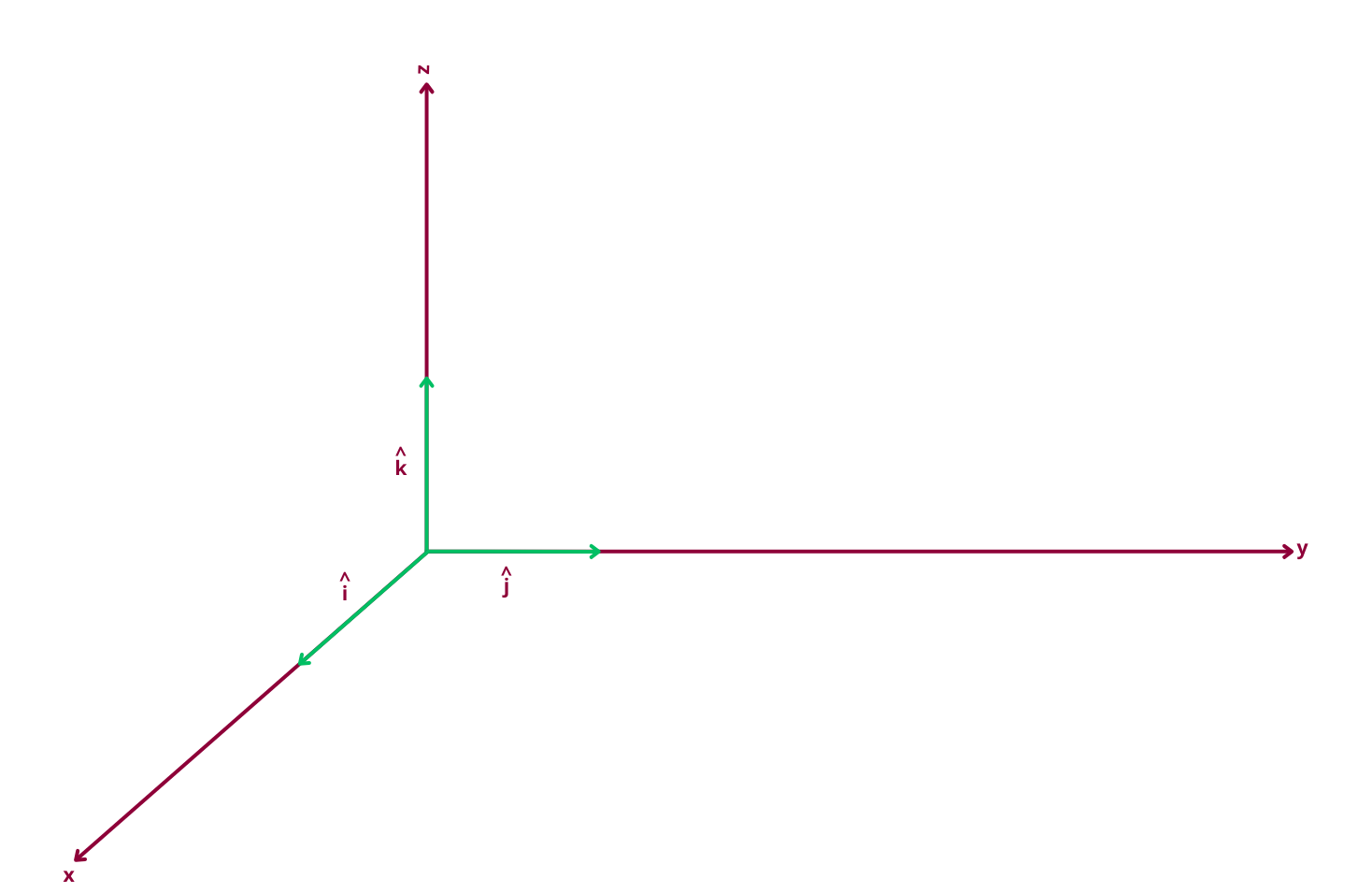
Unit Vectors in 3D Space

In 3D space, we use three unit vectors to show direction along the x-axis, y-axis and z-axis.

$\hat{i}\text{ - unit vector in the x-direction}$ $\hat{j}\text{ - unit vector in the y-direction}$ $\hat{k}\text{ - unit vector in the z-direction}$

These vectors each have a magnitude of 1:

$$\hat{i}=[1,0,0]\hat{j}=[0,1,0]\hat{k}=[0,0,1]$$

Unit vectors are used to build or describe other vectors. By scaling and combining them, we can express any vector in terms of direction and magnitude. Let’s go through a worked example.

A Worked Example

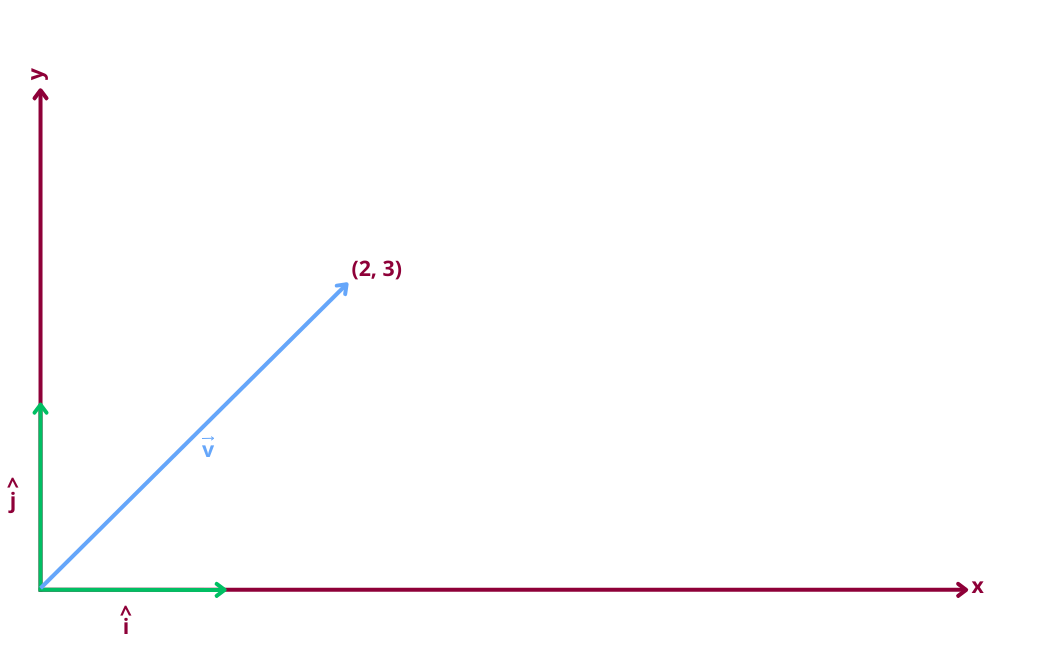
Suppose we have a vector in 2D space:

$$\overrightarrow{v}=[2,3]$$

This means the vector goes 2 units to the right and 3 units up.

We can express it using unit vectors:

$$\hat{i}=[1,0]\hat{j}=[0,1]$$

Using these, we write:

$$\overrightarrow{v}=2_{}\hat{i}+3_{}\hat{j}$$

This shows how any vector can be represented as a sum of scaled unit vectors.

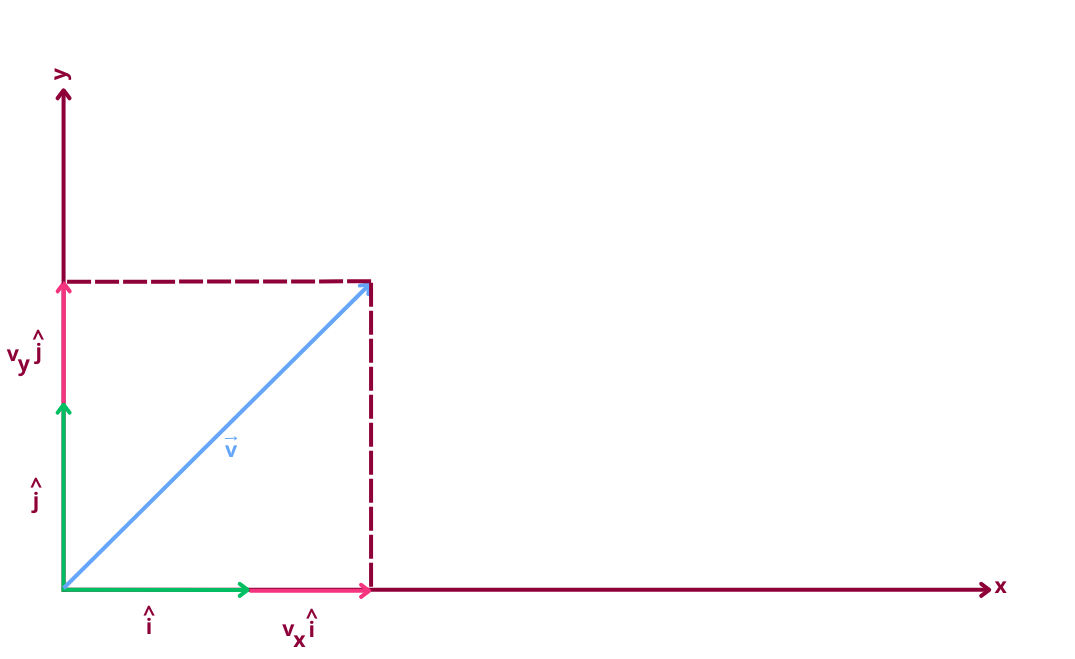
The head-to-tail method helps us visualize vector addition:

1. Start at the origin $(0,0)$
2. Move 2 units right → this is the vector $2\hat{i}$
3. From there, move 3 units up → this is the vector $3\hat{j}$
4. The tip now lands at $(2,3)$, which is the head of $\overrightarrow{v}$

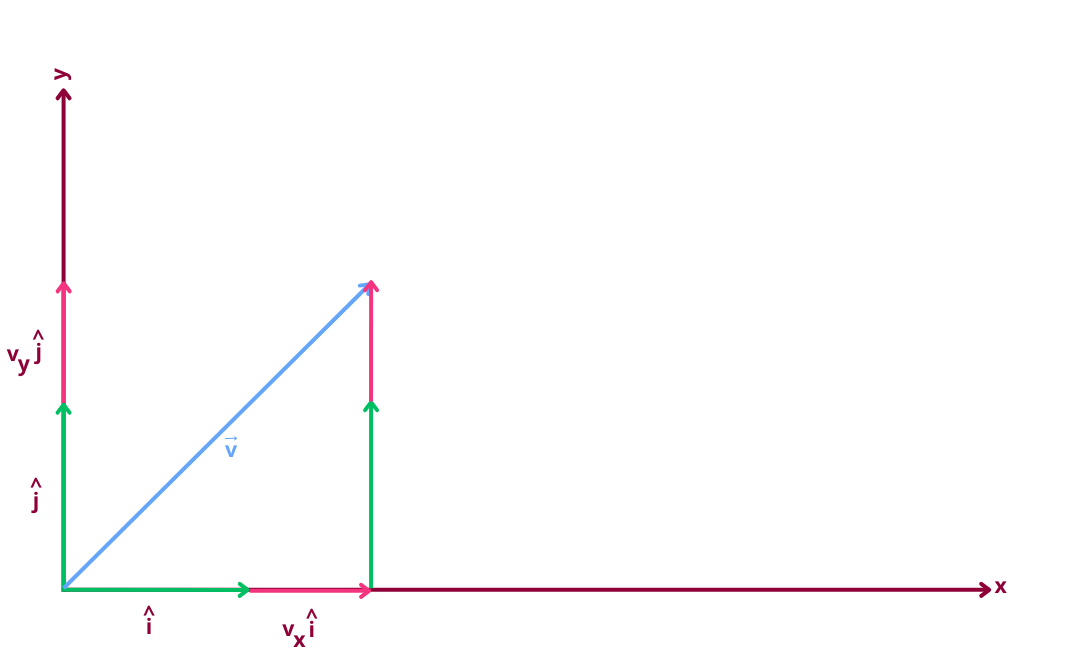
This method shows how vectors add together, especially when using unit vectors as building blocks.